Atmospheric escape - gas molecular mass

[zonkmachine]

In Pioneer the atmosphere is selected for one metric only, m_atmosOxidizing. The problem with this is that you end up with small bodies having atmospheres of predominantly light elements like H2 and He while in reality they are the first to be lost to atmospheric escape if the mass is too low and/or distance to the nearest star too close. Earth for instance can not hold on to H2 and He.



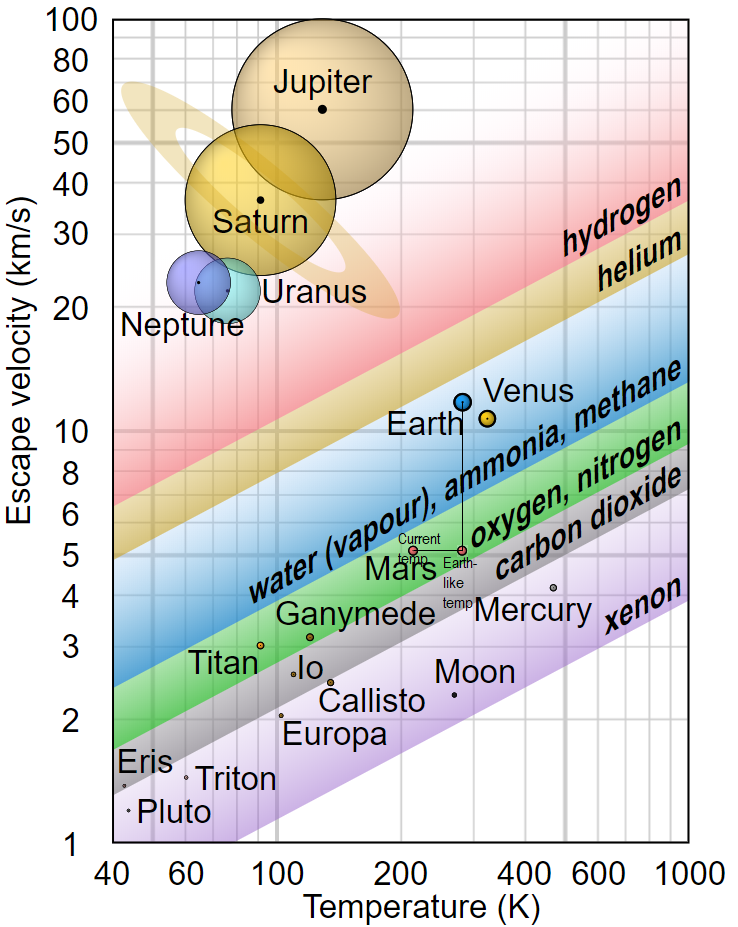
A graph showing the relationship of body mass/temperature and possible lowest molecule retained in the atmosphere. Here is a deeper discussion on the graph and why it's not quite correct but it still gives a hint to what's needed in the game. https://physics.stackexchange.com/quest ... ly-showing


In accrete, a program to simulate star system formation (Dole, 1970), the atmosphere is just presented as the lightest element that a body can retain. Example output:

Code: Select all

Planet #2:
   Distance from primary star (in A.U.):   0.405
   Eccentricity of orbit:                  0.027
   Mass (in Earth masses):                 0.145
   Equatorial radius (in Km):             3394.5
   Density (in g/cc):                      5.297
   Escape Velocity (in km/sec):             5.84
   Smallest molecular weight retained:     23.27   (N2)
   Surface acceleration (in cm/sec2):     502.53
   Surface Gravity (in Earth gees):         0.51
   Surface temperature (Celcius):         171.26
...

Fix: The fastest way to fix this is probably to let the atmosphere pass a second stage where mass and temperature is taken into account and the lower molecule weights is sieved out. The temperature referred to in the graph is the temperature of the lower thermopause (exobase) on thicker atmospheres and the surface temperature on thinner layers. Also, if you end up with a rare gas being the lightest element possible it would probably not be the bulk of the atmosphere. It would be better to present a more complete gas mixture instead of just one gas.

[impaktor]

For rabbit holes like these, it might be advisable to develop the model in separate program/language that allows fast development, simulation, and plotting/visualizaiton, before the final mechanics is ported to the core game engine.

Have a blast!